Most generative models for time series—particularly those borrowed from image generation—treat financial prices like any other numerical data: throw in Gaussian noise, then learn to clean it up.
But markets aren’t like pixels. Financial time series have unique structures: they evolve multiplicatively, exhibit heteroskedasticity, and follow stochastic dynamics that traditional diffusion models ignore.
In this week’s standout paper, “A diffusion-based generative model for financial time series via geometric Brownian motion,” Kim et al. propose a subtle yet profound twist: model the noise using financial theory, specifically geometric Brownian motion (GBM), rather than injecting it naively.
Injecting Theory into the Noise Itself
Score-based diffusion models typically add additive Gaussian noise over time and then learn to reverse this process. But additive noise assumes that volatility is constant across all prices—clearly wrong in finance. The volatility of $1,000 Tesla is not the same as $10 Ford.
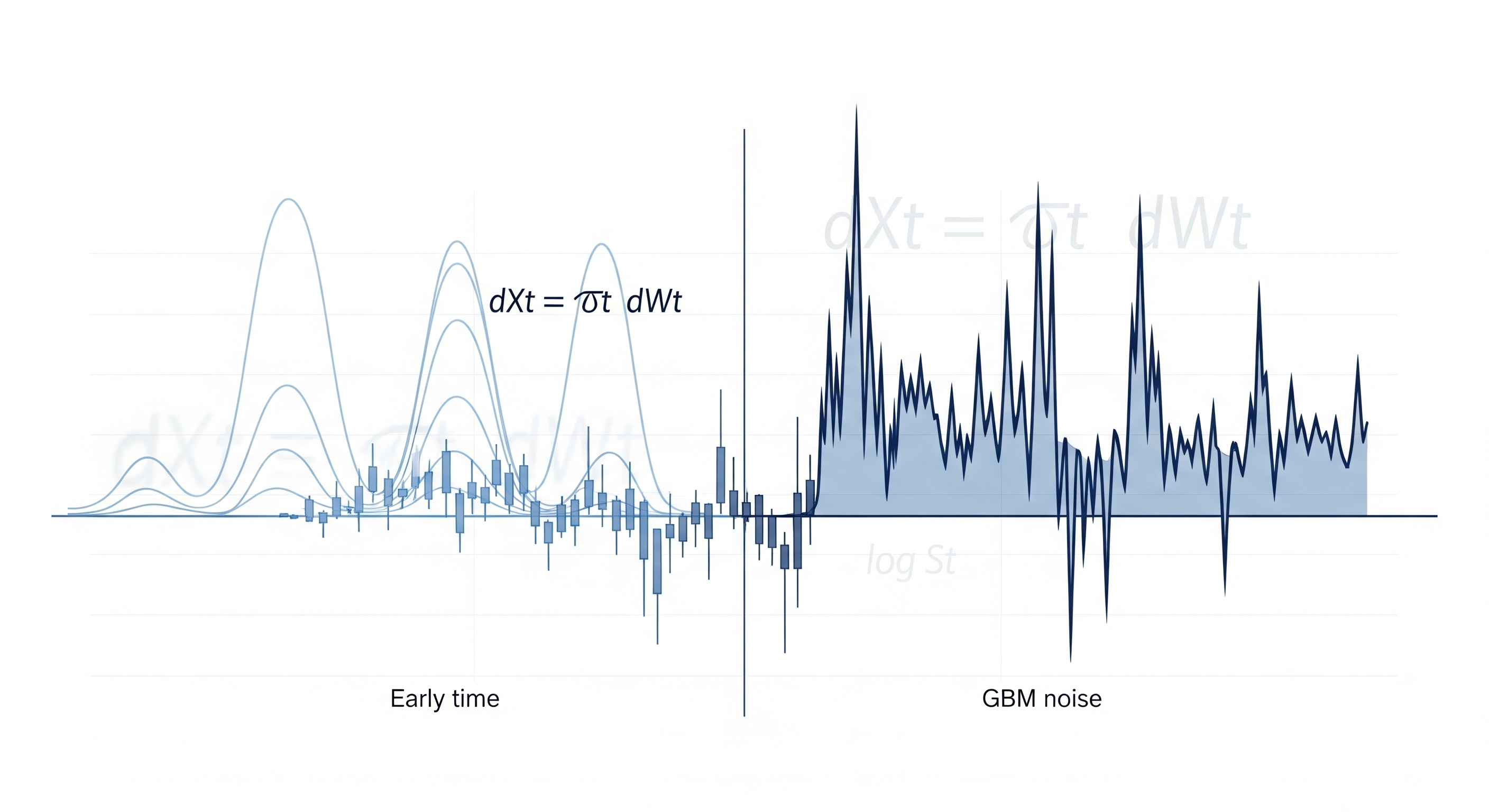
Kim et al.’s insight: inject noise in the log-price space using GBM principles, where noise scales proportionally with the price. In effect:
- Prices evolve as $ds = \mu s , dt + \sigma s , dW$
- Taking logs and eliminating drift, the model arrives at a variance-exploding SDE in log-price space: $dX_t = \sigma_t dW_t$
This aligns the forward noising process with real-world volatility behavior: state-dependent, not uniform.
| Traditional Diffusion | GBM-Inspired Diffusion |
|---|---|
| Additive noise in $x$ space | Multiplicative noise via log-prices |
| Assumes homoskedasticity | Captures heteroskedasticity |
| Ignores financial structure | Grounded in Black-Scholes theory |
Architecture: Transformer Meets Finance
The reverse-time denoising is handled by a Transformer-based score network, adapted from the CSDI model. Key tweaks include:
- Positional embeddings to track sequential structure
- Increased embedding dimensions to better capture the leverage effect
- Gated residual blocks for hierarchical feature extraction
Empirically, increasing the model’s capacity (128 conv channels, 256-d diffusion embedding, 64-d feature embedding) was crucial for capturing the asymmetry between negative returns and future volatility.
Benchmarking Against Reality
They evaluate synthetic time series on the classic stylized facts of finance:
-
Heavy-tailed returns: Captured well under GBM + exponential or cosine schedules, with tail exponent $\alpha \approx 3.0\text{–}4.6$, close to empirical $\alpha = 4.35$.
-
Volatility clustering: GBM yields long-range dependence in absolute returns, unlike VE/VP baselines.
-
Leverage effect: Only GBM-based models showed stable, negative lead-lag correlations consistent with real data.
| Stylized Fact | VE / VP Diffusion | GAN Baseline | GBM Diffusion |
|---|---|---|---|
| Heavy Tails | Too light ($\alpha > 8$) | OK | Matches empirical tail |
| Volatility Clustering | Short-range only | Noisy | Long-range power-law decay |
| Leverage Effect | Inconsistent | Erratic | Strong negative correlation |
From Modeling Prices to Modeling Noise
Perhaps the most interesting philosophical shift here is not just technical. Most financial models simulate prices using SDEs.
This paper models the noise process driving prices, reframing the problem: not “how do prices evolve?” but “how does noise shape evolution?”
It’s a subtle pivot, but it opens the door for hybrid models that combine:
- The statistical power of deep generative models, and
- The structural wisdom of financial theory
Where Next?
While this GBM-based approach doesn’t preserve exact log-normal marginals, it gets closer to what matters: trajectory realism. And the authors note future extensions could include rough volatility or conditioning on macro data.
For quant researchers and AI-finance builders, this paper offers a blueprint: use financial theory not just as a constraint on outputs, but as a guide for the noise that shapes everything.
Cognaptus: Automate the Present, Incubate the Future.