“In the absence of perfect knowledge, how do we still reason causally?”
This paper tackles a profound and practical dilemma in causal inference: what if we don’t know the full causal graph? In real-world settings — whether in healthcare, finance, or digital platforms — complete causal diagrams are rare. Practitioners instead rely on causal abstractions: simplified, coarse-grained representations that preserve partial causal knowledge. But this raises a fundamental question: Which causal queries can still be identified under such abstraction?
Yvernes et al. (CAR @ UAI 2025) propose a powerful response: a hierarchy of identifiability criteria for causal queries when only a collection of plausible causal graphs is known. Their framework not only connects diverse past approaches but also introduces new conceptual clarity, enabling practitioners to navigate uncertainty with precision.
From One Graph to Many: Why Abstraction Matters
Classical causal inference — rooted in Pearl’s do-calculus — assumes we know the full Directed Acyclic Graph (DAG) of variables. This is often unrealistic. Instead, many modern applications rely on causal abstractions, such as Partial Ancestral Graphs, Markov Equivalence Classes, or summary graphs. These do not fix a unique causal model but rather define a collection $\mathcal{C}$ of compatible graphs.
The central task is to determine whether a causal query $P(y,|,\text{do}(x), z)$ is identifiable across all graphs in $\mathcal{C}$. The challenge is that different graphs may yield different estimands — and our goal is to find criteria under which they yield the same one.
The Hierarchy: A Map of Identifiability Notions
The authors define four main notions of identifiability for causal abstractions, ordered from strongest to weakest assumptions:
| Abbreviation | Name | Requires Knowledge of | Requires Common Proof? | Notes |
|---|---|---|---|---|
| IGP | Identifiable through Graphs w/ P(V) | Full observational dist. | No | Most information; can distinguish SCMs with same graph structure. |
| IG | Identifiable through Graphs | Graphs only | No | Requires same estimand across all graphs in $\mathcal{C}$. |
| ICD | Identifiable by Common Do-Calculus | Graphs only | Yes | A single do-calculus proof must apply to all graphs. |
| ICGC | Identifiable by Common Graphical Criterion | Graphs only | Yes (via backdoor/frontdoor) | Easiest to check but weakest in coverage. |
This hierarchy is not merely conceptual — it is operational. If you can’t prove IGC, try ICD. If ICD fails, ICGC might still hold.
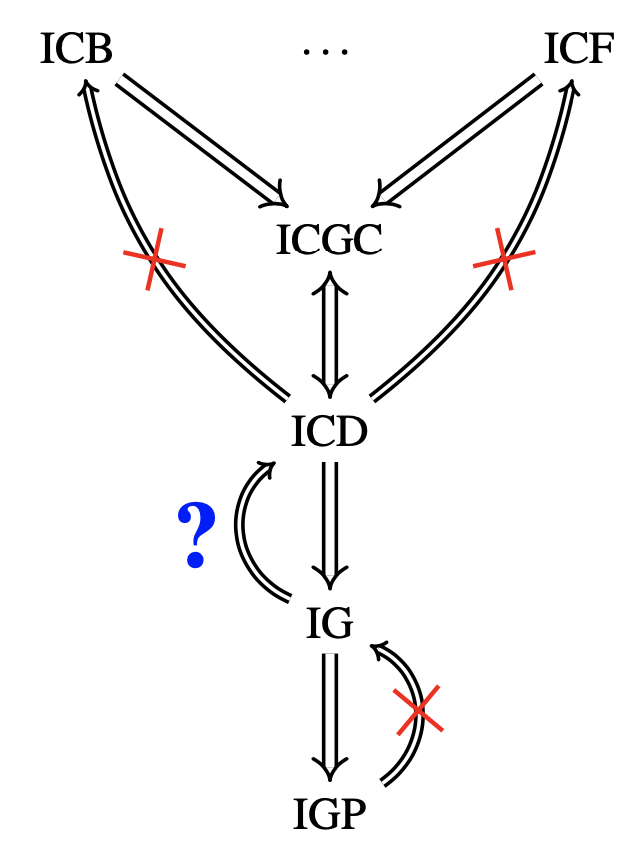Figure: Logical implications among identifiability criteria. An arrow indicates that the implication holds in every case. A red cross on an arrow indicates that the implication fails in at least one case. A blue question mark on an arrow indicates that the validity of the implication is still open.
A Smart Trick: Focus on Maximal Graphs
One of the most practically useful results is Theorem 2: if a causal query is identifiable in the maximal elements of a graph collection $\mathcal{C}$, it is identifiable in all of $\mathcal{C}$.
This is based on the intuition that removing edges from a graph only reduces dependency information. So if your identification method works in the most connected (maximal) cases, it still works in sparser ones.
This is especially important when $\mathcal{C}$ is large or infinite — such as when representing uncertainty about causal directionality. For example, in Cluster DAGs, the authors show that there’s often a unique maximal graph, collapsing the identifiability check to a single model.
A Puzzle Remains: Is IG Stronger than ICD?
Despite the tidy hierarchy, one link remains unresolved: Can identifiability through graphs (IG) ever occur without a common do-calculus proof (ICD)?
The authors conjecture yes, and propose how such a counterexample might be constructed — involving two different valid do-calculus proofs yielding the same estimand, but no single proof working for both graphs.
This question is more than academic: proving this separation would show that identifiability may sometimes be achievable only by reasoning individually over each graph, not through a unified calculus. That would have major implications for the design of causal inference algorithms in uncertain environments.
Implications for Practitioners
- Causal inference under abstraction is not binary: You can navigate different levels of certainty by understanding which identifiability criterion you meet.
- Do-calculus is powerful but not always required: Some queries are identifiable just by checking simpler graphical criteria across all graphs.
- Maximal graphs are your friends: Focus your computational effort there.
- Know when data helps: IGP shows that knowing the observational distribution can sometimes unlock identifiability where graphs alone cannot.
Closing Thoughts
This framework offers a timely blueprint for causal reasoning in complex domains where full graphs are unavailable. By embracing abstraction — but structuring it — we gain both flexibility and rigor.
Cognaptus is particularly interested in this for use cases like customer journey modeling, healthcare diagnostics, and marketing uplift modeling, where causal effects must be estimated under uncertainty. Integrating this hierarchy into AI-powered decision systems could dramatically improve robustness and transparency.
Cognaptus: Automate the Present, Incubate the Future.