If you’re tired of classical GANs hallucinating financial time series that look right but behave wrong, you’re not alone. Markets aren’t just stochastic — they’re structured, memory-laced, and irrational in predictable ways. A recent paper, Quantum Generative Modeling for Financial Time Series with Temporal Correlations, dives into whether quantum GANs (QGANs) — once considered an esoteric fantasy — might actually be better suited for this synthetic financial choreography.
The Stylized Trap of Financial Time Series
Financial time series — like S&P 500 log returns — aren’t just heavy-tailed and non-Gaussian. They also exhibit temporal quirks:
- Volatility Clustering: Wild days follow wild days; calm follows calm.
- No Linear Autocorrelation: Predictable returns are arbitraged away.
- Leverage Effect: Downturns trigger higher volatility.
These patterns, dubbed stylized facts, are rarely preserved by generative models trained only to match distributions.
Enter the Quantum Generator
The authors replace the classical GAN generator with a Parameterized Quantum Circuit (PQC) that samples expectation values from Pauli-X and Pauli-Z measurements. These values, post-processed, become log return sequences.
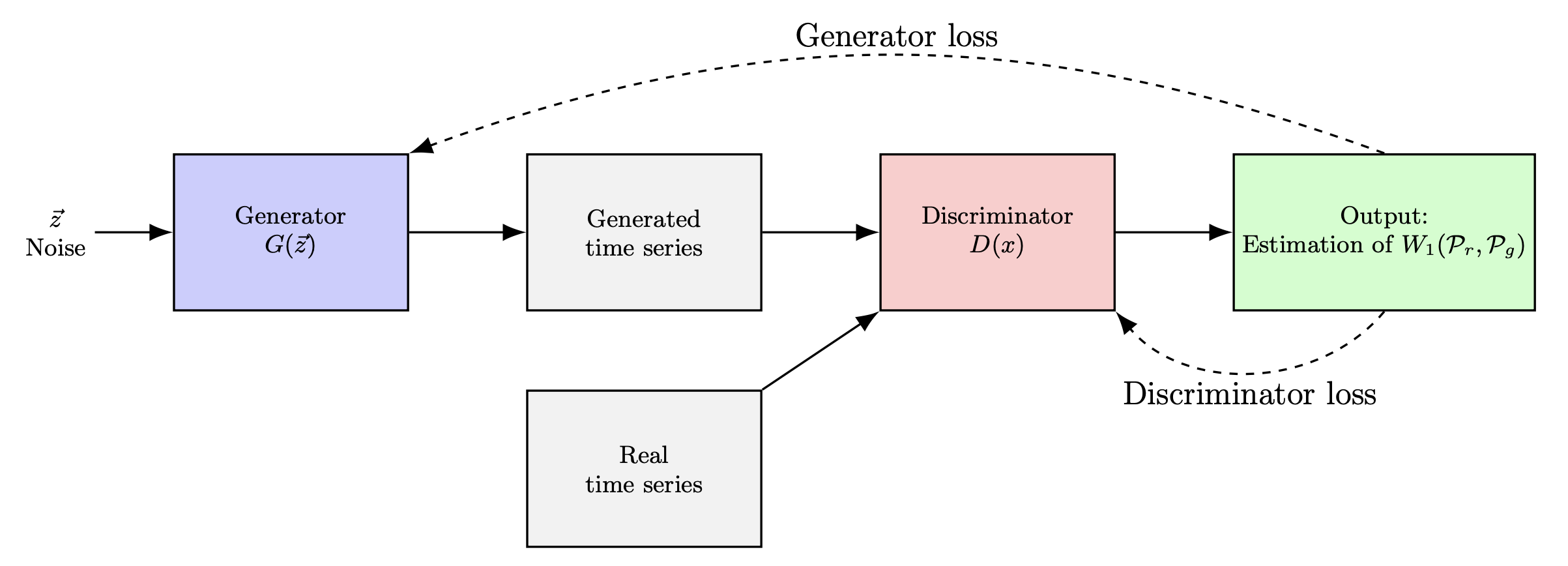
The discriminator remains classical — a CNN trained with Wasserstein loss + gradient penalty for stability.
Why Quantum?
Quantum circuits can represent probability distributions that are provably hard for classical models. But the real question isn’t superiority — it’s suitability. Do QGANs carry inductive biases that mirror real market mechanics?
Two Simulation Regimes: Exact vs Efficient
To explore this, the authors use:
- Full-state simulation (exact, but scales as $2^n$)
- Matrix Product State (MPS) simulation (approximate, but tunable via bond dimension)
| Simulation | Qubits | Layers | Bond Dim | EMD (dist match) | Volatility Clustering |
|---|---|---|---|---|---|
| Full-state | 10 | 8 | N/A | 2.4e-4 | 0.15 |
| MPS | 10 | 18 | 32 | 3.1e-4 | 0.29 |
| MPS | 20 | 6 | 70 | 4.2e-3 | 0.99 |
The best results came from 10-qubit MPS simulations with deeper circuits (18 layers) and moderate bond dimension (32), suggesting a sweet spot between expressivity and overfitting.
Stylized Facts: Quantified
To evaluate how well QGANs mimic reality, they define four metrics:
- EMD: Earth Mover’s Distance between distributions
- $EACF_{id}$: Identity autocorrelation (should be near 0)
- $EACF_{abs}$: Absolute autocorrelation (captures volatility clustering)
- ELev: Correlation between squared returns and lagged returns (leverage effect)
Lower is better across the board. In their top models, all metrics were significantly improved over classical GAN baselines.
Clever Preprocessing: A Classical Assist
Interestingly, the paper also applies a Lambert-W transform during preprocessing to squash heavy tails into Gaussian-like shapes before quantum learning. This hybrid wisdom — letting classical tricks help quantum systems — points toward a pragmatic future: quantum-classical synergy, not competition.
The Bigger Picture
While training QGANs remains costly and scaling is limited by barren plateaus, this paper makes one point clear: quantum models can implicitly capture complex temporal dependencies — without being explicitly trained to do so. That’s not magic. That’s inductive bias.
It’s an exciting glimpse into what quantum machine learning might mean for finance: not just speedups, but structure.
Cognaptus: Automate the Present, Incubate the Future
