Can we prove that we understand how a transformer works? Not just describe it heuristically, or highlight patterns—but actually trace its computations with the rigor of a math proof? That’s the ambition behind the recent paper Mechanistic Interpretability for Transformers: A Formal Framework and Case Study on Indirect Object Identification.
The authors propose the first comprehensive mathematical framework for mechanistic interpretability, and they use it to dissect how a small transformer solves the Indirect Object Identification (IOI) task. What results is not just a technical tour de force, but a conceptual upgrade for the interpretability field.
From Heuristics to Hypotheses
Historically, interpretability has relied on visualizations, probing classifiers, and a heavy dose of intuition. This paper instead formalizes interpretability as a subgraph isomorphism problem. In simple terms: to say we “understand” a behavior, we must construct a computational graph (a circuit of attention heads, neurons, etc.) that mirrors the actual computation inside the model—with high fidelity.
Their proposed workflow follows a scientific method:
- Hypothesize a motif (e.g. an attention head copying a subject token).
- Trace how it flows through the model layers.
- Match this against the model’s computation.
- Verify via substitution or ablation: remove or replace parts and observe changes.
This turns interpretability into something falsifiable. Either your circuit explains the behavior—or it doesn’t.
Case Study: Who Got the Book?
The IOI task is syntactically subtle. Given a sentence like:
John gave Mary the book because she asked.
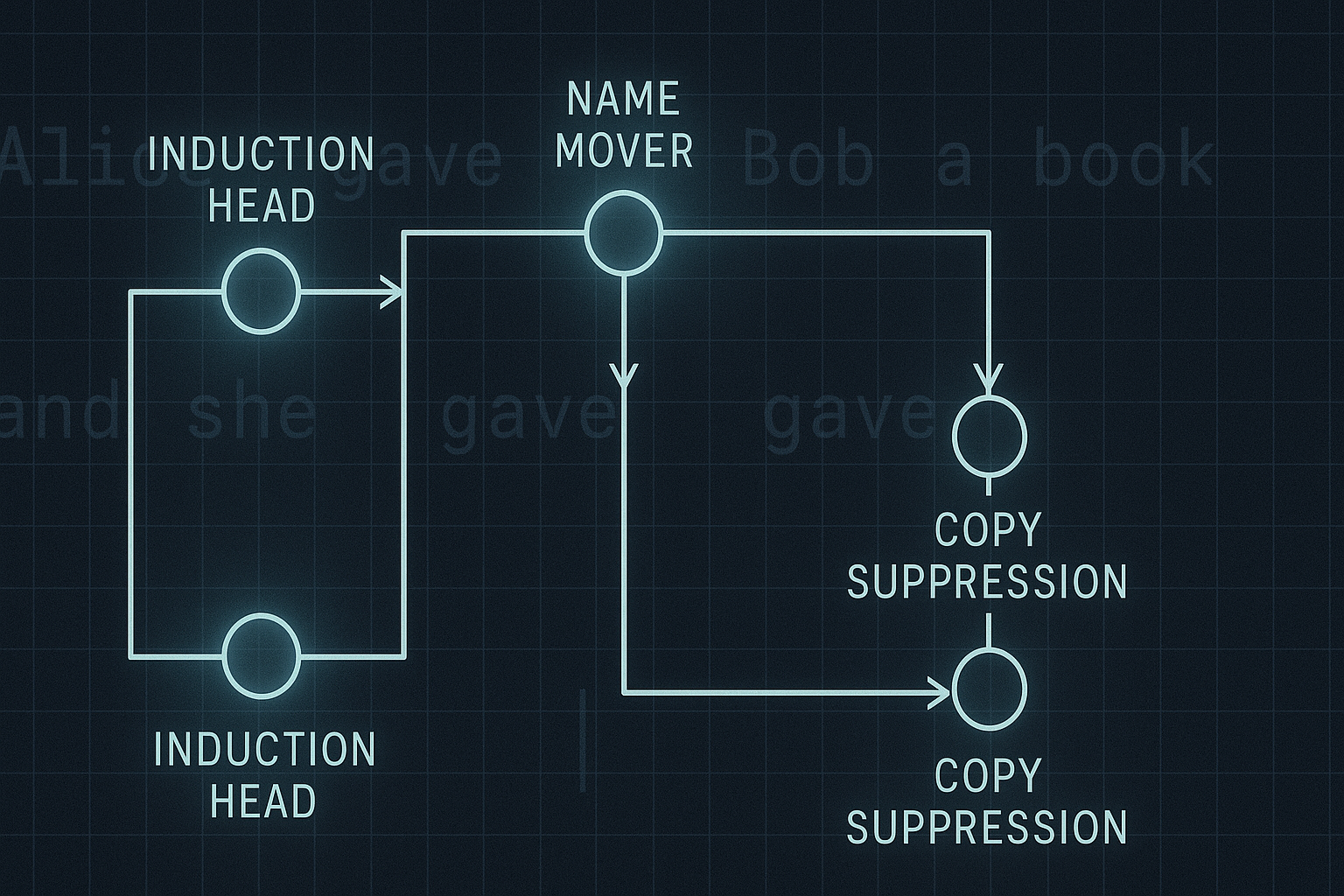
A model must determine that “Mary” is the indirect object being referred to. The authors trained a 2-layer, 4-head transformer and achieved near-perfect accuracy. But more impressively, they could map 95% of that accuracy to a specific 5-head circuit using their formal framework.
The Cast of Heads:
| Layer | Head Type | Function |
|---|---|---|
| 0 | Induction | Identifies syntactic links between subject and pronoun |
| 1 | Induction | Reinforces the pairing (e.g. “Mary” → “she”) |
| 1 | Copy Suppression | Suppresses distractor tokens (like “John”) |
| 1 | Name Mover | Transfers relevant name to the output position |
| 1 | Output Copier | Final head ensuring correct token at output |
Each head’s role is carefully dissected through path patching, residual stream tracing, and activation substitutions.
Interpretability as Engineering Discipline
Why does this matter beyond academic elegance?
- It gives us reproducibility: other researchers can audit, extend, or falsify the proposed circuit.
- It enables modular understanding: one could replace heads or sub-circuits with human-written logic.
- It creates a roadmap for scaling: though done on a small model, the method is scalable in principle, especially with automation.
In many ways, this mirrors the evolution of early electronics: from black-box devices to circuit diagrams.
A Call for Rigorous Transparency
The broader message is this: if we want to trust, align, and govern powerful language models, we must hold ourselves to a higher standard of clarity. Not just what the model outputs, but how it gets there—down to individual components.
This paper doesn’t just interpret a model. It models interpretation itself as a mathematical exercise. That’s a step-change in how we think about transparency.
Cognaptus: Automate the Present, Incubate the Future